Antenna specifications can seem confusing or, worse yet, can be misinterpreted. Of all the salient antenna specifications, antenna gain appears to present the biggest problem. Some understand the antenna gain provided in datasheets to be valid in the so-called far field region. However, EMC radiated immunity tests do not force using antenna far field operation in many instances. What is the far field region, what does the term far field imply, where is the far field boundary, why is there a debate over the definition of the far field boundary, and how can one apply this far field information to their situation, are all topics that remain unclear to some.
The far field region is generally understood as a region, far enough away from a radiating source, where the radiation pattern does not change shape as the distance increases. In other words, the angular distribution of energy does not vary with distance. Furthermore, the far field wave consists of electric and magnetic field components which are orthogonal to each other and the direction of propagation. The ratio of electric and magnetic field components is the wave impedance in a broad sense. Some say the far field is the region where the impedance has stabilized at 377 Ohms.
The term far field implies a region exists closer to a radiating source, where the radiation pattern changes as a function of distance from the antenna and the wave impedance is not stable. There should also be a boundary between the near field and far field regions. However, the boundary is more of a gradient providing a gradual transition between the regions, therefore attempts to characterize the real-world boundary location using mathematical equations commonly produce different results.
According to an EMC Engineer at an auto parts company, a group of engineers were discussing when someone posed the question, “When does a product find itself in the far field of a radiation source?” They soon realized they were not all in agreement on where this boundary was in relation to the radiating source. One engineer said the far field began at a distance of 3λ, where λ is the wavelength of the radiation. The next engineer claimed the far field begins at
Yet another engineer gave his definition, saying the far field begins at
Finally, since the last engineer knew the “correct” answer, he chimed in with
where D is the largest physical dimension of the antenna.
It became clear that what each of these engineers knew to be true was up for debate; however, could they all have been correct?
Wavelengths are very large at very low frequencies, and many antennas will appear electrically small. A general “rule of thumb” whether a product finds itself in the far field is to multiply the wavelength, λ, by three; however, this only holds true for electrically short antennas or those whose dimensions are less than one-half of the wavelength. If the product is further than 3λ away from an electrically short antenna, then it is likely in the far field.
Using Maxwell’s equations, SA Schelkunoff derived equations that described the fields from a small electric dipole antenna as follows:
and
Where:
I = the wire current in amps
L = the wire length in meters
β = the electrical length per meter of wavelength, ω/c, or 2*π/ λ
ω = the angular frequency in radians per second, or 2*π*f
ε₀ = the permittivity of free space
θ = the angle between the wire axis and the observation point
f = the frequency in Hertz
c = the speed of light, or 3*10⁸ m/sec;
r = the distance from the source to the observation point in meters
By setting the magnitudes of the two terms in the square-brackets of equation (2) equal, the result will return the boundary point for which we are searching:
Substituting the definition of β, we obtain the boundary for dipole antennas as a function of wavelength:
Another approach to defining the boundary is analyzing the wave impedance as a function of distance from the source. Considering an electrically short dipole and loop antenna, one can plot the wave impedance as a function of wavelengths from its source, as seen in Figure 1.
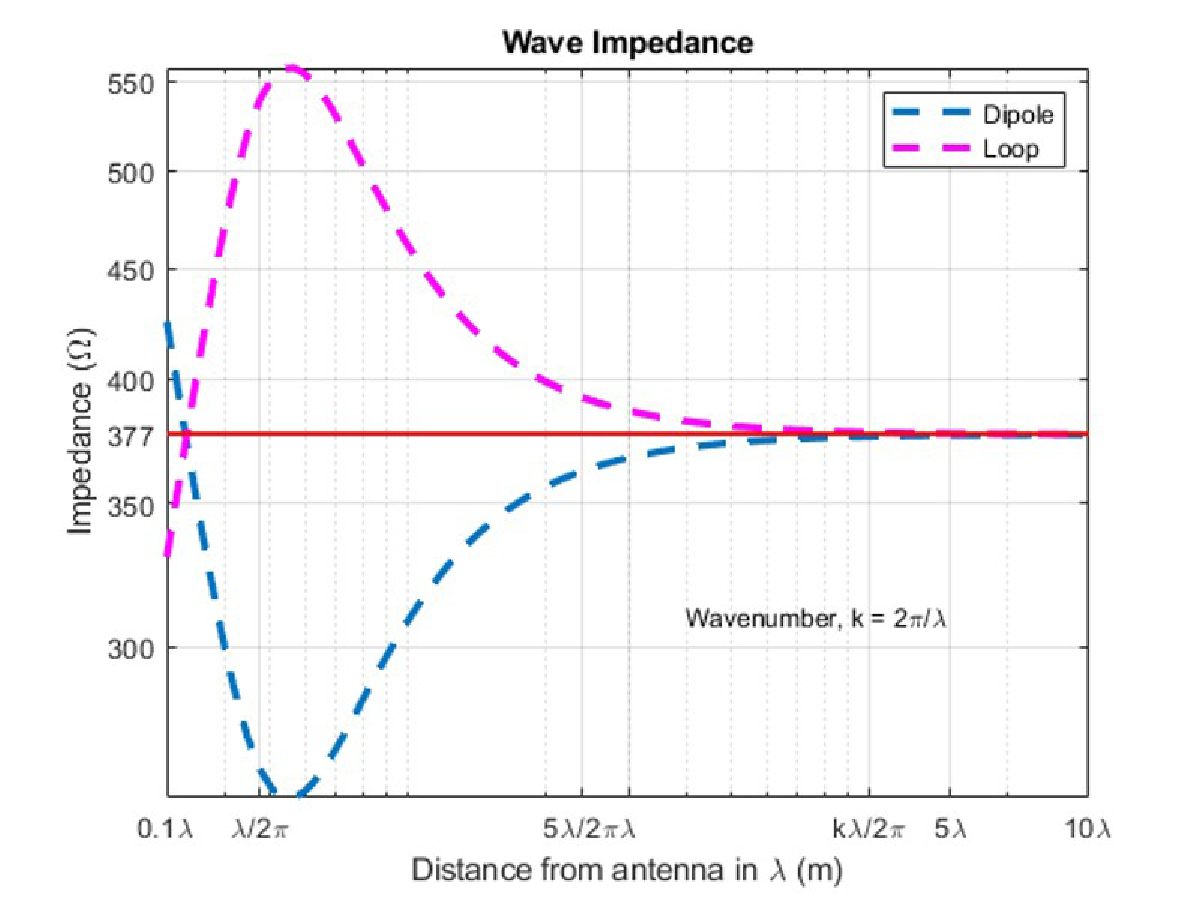
In the far field, the field is dominated by electric or magnetic fields with electric dipole characteristics, while the near field is considered a collection of dipoles with a fixed phase relationship. The ratio of electric and magnetic field intensities turns out to be the wave impedance in the far field. Whereas the electric and magnetic fields can exist independently of each other in the near field, and one type can dominate the other.
Observing at λ/2π for the electric dipole, whose dominant radiation mechanism is via an electric field, shows a local minimum whose value is not 377 Ohms. From the wave impedance perspective, a better approximation of the far field distance is 5λ/2π. The 5λ/2π definition is beneficial for shield designers because the ratio of the shield’s impedance to the field’s impedance determines the amount of protection the shield provides (C. Capps).
Depending on the application, it may be more appropriate to use one definition of far field as opposed to another. Specifically, the following two definitions are commonly accepted for many commercial and military test standards approximating far field distances. These equations depend on the size of the antenna being used and the wavelength of the radiating wave. When the wavelength is much larger than the antenna, as is for a majority of dipole or log-periodic antennas, the first equation is used. Conversely, the second equation should be used when the wavelength is smaller than the antenna, like with horn antennas.
When D << λ:
When D >> λ:
Where:
r = far field distance in meters
λ = wavelength of the radiating wave in meters
D = largest dimension of the antenna’ s radiating aperture that is orthogonal to the direction of propagation in meters.
One can see the relationship between frequency and far field distance by observation. The far field distance is directly proportional to the wavelength in the first case for a dipole or log-periodic antenna.
In other words, as the frequency increases, the wavelength decreases and, since the wavelength is directly proportional to far field distance, the far field distance also decreases.
In the equation for horn antennas, the wavelength is in the denominator; therefore the far field distance is inversely proportional to the wavelength.
As the wavelength decreases, the numerator is divided by a smaller and smaller number resulting in an increasing far field distance.
Consider the following: a technician is performing a radiated susceptibility test in accordance with MILSTD- 461, test method RS103. The technician installs a horn antenna for generating electric fields above 1 GHz. The largest dimension, orthogonal to the direction of propagation, is 0.18 m, and the highest frequency of test is 18 GHz.
At 1 GHz, the wavelength is
therefore, the far field boundary is
from the antenna. At 18 GHz, the wavelength is
therefore, the far field boundary is
from the antenna. Therefore, we can see that as the frequency increases, the far field boundary moves further from the antenna.
Regardless of the type of test and standard being applied, it is important to know whether requirements specify testing at a near field or far field distance. A test subject will find itself in the near field in most cases. Testing in the far field often requires large distance requirements that most laboratories may find difficult to satisfy.
One should ask several questions when selecting an antenna for any given test method. Some examples are:
While the priority is to meet the requirements given by the standard, selecting the right antenna can be a balancing act. The antenna and the test equipment setup shall meet the standard’s requirements; however, the antenna should also provide enough coverage and gain to allow for efficient testing of the EUT. When possible, it is always beneficial to have a variety of antennas to select from to perform a test.
160 Schoolhouse Rd.
Souderton PA 18964-9990 USA
215.723.8181
[email protected]
[email protected]
Contact Us
For an applications engineer call:
800.933.8181
For Customer Service, call:
215.723.0275
For Faxing Orders:
866.859.0582 (Orders Only, Please)
Privacy Policy
Terms of Use
Transparency in Coverage (TCR)
Copyright ©2023 AR Inc.